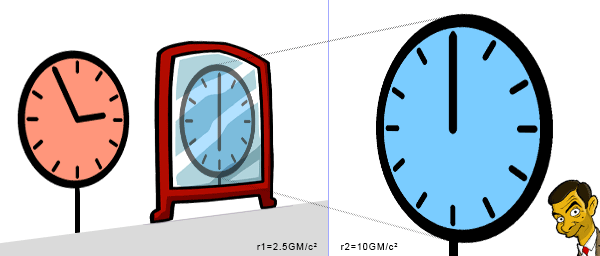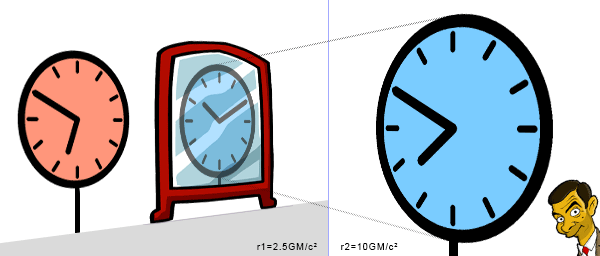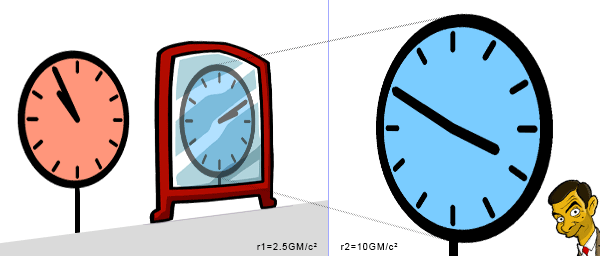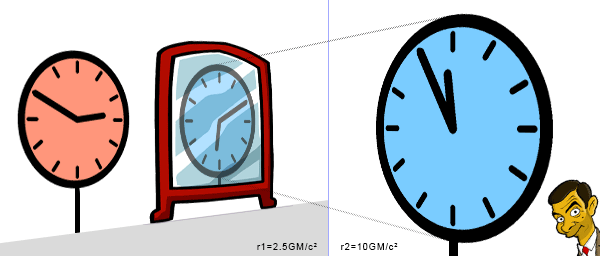
Yukterez hat geschrieben:Neue Kopfnuss: In Bild 1 sehen wir dass der Beobachter bei r2=10GM/c² das Spiegelbild im Spiegel auf r2=2.5GM/c² im Vergleich zu seiner lokalen Uhr um 6h nachgehen sieht. Wie hoch muss die Masse M sein damit sich das hin und zurück ausgeht? 10 Reputationspunkte ausschreibend,...
Die Lösung der Differentialgleichung für die Koordinatengeschwindigkeit
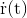
des Photons mit Abhängigkeit von seiner Startposition
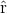
und der Schalenposition
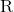
des Beobachters in dessen System wir das Szenario beschreiben
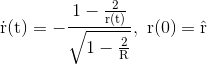
lautet für die zeitabhängige Position des Photons
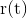
in den natürlichen Einheiten
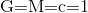
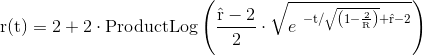
Um die von der Zielposition

abhängige Lichtreisezeit
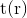
im System unseres Schalenbeobachters zu erhalten stellen wir um auf
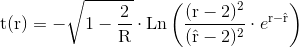
Jetzt setzen wir die Bedingungen für die Beobachterposition und den Start- und Endpunkt des Photons ein:
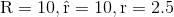
und erhalten
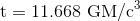
Dann benötigen wir noch die folgenden Zahlen:
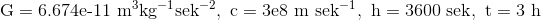
und können bequem nach
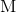
auflösen:
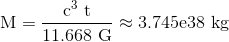
Das wäre also eine relativ hohe Masse von ca. 187 Millionen Sonnenmassen, was im Fall eines schwarzen Lochs einer durchschnittlichen Dichte von grob 520 kg/m³ entspräche.
Trostpreisfrage: wie hoch müsste die Masse unter Newton sein damit es sich mit 6 Stunden hin und zurück genau ausginge?
Die 10 Punkte diesmal selbst einstreichend, aber dafür weitere 5 ausschreibend,
 Da der Latex-Server gestern gleich zwei mal kurz gesponnen hat hier zur Sicherheit das Backup des Beitrags als Screenshot.
Da der Latex-Server gestern gleich zwei mal kurz gesponnen hat hier zur Sicherheit das Backup des Beitrags als Screenshot.